Please also see the Python version of this article. To skip straight to the code, please check out The Crosstab Kite’s gists repo.
Decision-makers often care deeply about how long it takes for some key event to happen.
- In business, how long until a user generates revenue? How long until a user churns from a subscription service? How long until a new product achieves traction?
- In medicine, how long until patients leave the hospital, experience a recurrence of disease, or die?
- With hardware, how long until a piece fails?
Analytics tables and dashboards rarely answer these questions directly and correctly. Why? Because the survival analysis methods that best answer these questions are implemented in R and Python packages that can’t be incorporated into SQL-based data pipelines and dashboards.
In this article, I show how to compute survival curves and cumulative hazard curves directly in SQL (Postgres, specifically). Please copy and use the code in this post—let me know if you find it useful! You can also find the code with a permissive license in The Crosstab Kite gists repo.
This post assumes you know what survival and cumulative hazard curves are and why you would want to estimate them. For an intro to these concepts, I recommend the documentation for the Lifelines and Scikit-survival packages, and you should also check out my other articles on survival analysis.
The data context
I’ll use the Retail Rocket dataset, which I downloaded from Kaggle. This dataset is an event log, where each row represents an interaction between a Retail Rocket user (visitorid) and a product (itemid) at a moment in time (event_at). Here’s a sample:
visitorid | event_type | itemid | transactionid | event_at
-----------+-------------+--------+---------------+----------------------------
483717 | view | 253185 | | 2015-06-01 22:12:35.914-07
105775 | addtocart | 312728 | | 2015-06-01 21:54:40.956-07
951259 | view | 367447 | | 2015-06-01 22:02:17.106-07
972639 | view | 22556 | | 2015-06-01 22:48:06.234-07
404403 | transaction | 150100 | 5216 | 2015-06-01 11:19:32.71-07This dataset contains three types of user actions. The user can view a product (view), they can add a product to their cart (addtocart), or they can buy a product (transaction).
We’re interested in how long it takes users to make their first purchase.
The complication is that the data are right-censored. Most users didn’t make any purchases at all and there’s no way for us to know if that’s because they’ve decided not to or they just haven’t had enough time. Survival analysis gives us the tools to deal with this problem.
Before we get to the methods, though, we have to work through a couple of intermediate data tables.

First, we need to aggregate the event log into a duration table, which is the starting point for most survival analysis methods, including my SQL query below. Each row of a duration table represents a study subject (e.g. a Retail Rocket user). The essential fields are:
subject ID
outcome indicator: indicates whether or the subject experienced the target outcome during the study.
duration: how long it took for the subject to experience the target outcome, if applicable, or for the observation window to close, relative to that subject’s start time. For subjects that didn’t experience the target outcome, we still know it took at least as long as this value for the outcome to occur.
I showed how to construct duration tables from event logs in a previous article. Here’s a snippet of the duration table for the Retail Rocket example that came out of that post:
visitorid | endpoint_type | duration
-----------+---------------+-----------------------
170 | | 113 days 01:23:01.844
171 | | 71 days 09:10:28.034
172 | transaction | 31 days 21:57:44.591
173 | | 47 days 01:02:08.16The endpoint_type column is the outcome indicator; null values mean the subject has not yet made any purchases.
The full query
The following query starts with the duration table described above. It first computes a survival table then uses the survival table to compute the Kaplan-Meier survival curve and the Nelson-Aalen cumulative hazard curve.
Here’s the full query, for context and easy copying. In the following sections, I’ll break it down and explain each Common Table Expression (CTE) and the final SELECT statement individually. I’m using Postgres 12.7 on Ubuntu 20.04.
CREATE TABLE survival AS
WITH num_subjects AS (
SELECT COUNT(1) AS num_subjects FROM durations
),
duration_rounded AS (
SELECT
visitorid,
endpoint_type,
ceil(extract(epoch FROM duration)/(24 * 60 * 60)) AS duration_days
FROM durations
),
daily_tally AS (
SELECT
duration_days,
COUNT(1) AS num_obs,
SUM(
CASE
WHEN endpoint_type IS NOT NULL THEN 1
ELSE 0
END
) AS events
FROM duration_rounded
GROUP BY 1
),
cumulative_tally AS (
SELECT
duration_days,
num_obs,
events,
num_subjects - COALESCE(SUM(num_obs) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND 1 PRECEDING), 0
) AS at_risk
FROM daily_tally, num_subjects
)
SELECT
duration_days,
at_risk,
num_obs,
events,
at_risk - events - COALESCE(lead(at_risk, 1) OVER (ORDER BY duration_days ASC), 0) AS censored,
EXP(SUM(LN(1 - events / at_risk)) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND current ROW)
) AS survival_proba,
100 * (1 - EXP(SUM(LN(1 - events / at_risk)) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND current ROW))
) AS conversion_pct,
SUM(events / at_risk) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND current ROW
) AS cumulative_hazard
FROM cumulative_tally
WHERE events > 0Here are the first and last five rows of the created table:
duration_days | at_risk | num_obs | events | censored | survival_proba | conversion_pct | cumulative_hazard
---------------+---------+---------+--------+----------+----------------+----------------+-------------------
0 | 1407580 | 118 | 118 | 0 | 0.9999 | 0.0083 | 0.0000
1 | 1407462 | 14536 | 9451 | 5085 | 0.9932 | 0.6798 | 0.0067
2 | 1392926 | 5860 | 379 | 5481 | 0.9929 | 0.7068 | 0.0070
3 | 1387066 | 9605 | 172 | 9433 | 0.9928 | 0.7191 | 0.0071
4 | 1377461 | 11092 | 133 | 10959 | 0.9927 | 0.7287 | 0.0072 duration_days | at_risk | num_obs | events | censored | survival_proba | conversion_pct | cumulative_hazard
---------------+---------+---------+--------+----------+----------------+----------------+-------------------
124 | 156580 | 11086 | 1 | 11085 | 0.9912 | 0.8724 | 0.0087
125 | 145494 | 10196 | 1 | 45118 | 0.9912 | 0.8731 | 0.0087
129 | 100375 | 11691 | 2 | 11689 | 0.9912 | 0.8751 | 0.0087
130 | 88684 | 9011 | 1 | 9010 | 0.9912 | 0.8762 | 0.0087
131 | 79673 | 6990 | 1 | 79672 | 0.9912 | 0.8775 | 0.0087Breakdown: from durations to survival table
The second intermediate table we need to build is the survival table. Whereas the rows of the event log represent events and the rows of the duration table represent subjects, the rows of a survival table represent durations of time. The fields of the table count three things for each duration:
The number of study subjects still at risk of experiencing the target outcome event. The term at risk is standard but confusing; in the Retail Rocket example, it’s the number of users who have not yet made a transaction. Those users are still at risk of making their first transaction, so to speak.
The number who experienced the target outcome at exactly that duration.
The number who were censored at some point between the current duration and the next duration.
Let’s walk through the query steps before looking at the result. In all of the following snippets, I’ve omitted the CTE names and LIMIT clauses.
The first CTE is num_subjects, which—not surprisingly—counts the number of study subjects.
SELECT COUNT(1) AS num_subjects FROM durationsThe second CTE is duration_rounded. Its primary purpose is to convert the duration field in the input table from an interval type to a numeric type field duration_days. The simplest way I found to do this is to first convert the interval to elapsed epoch seconds with the EXTRACT function, then divide by the number of seconds in a day: 24 * 60 * 60.
SELECT
visitorid,
endpoint_type,
ceil(extract(epoch FROM duration)/(24 * 60 * 60)) AS duration_days
FROM durationsThe next CTE is daily_tally; this is where the row meaning changes from individual subjects to time durations, via the GROUP BY on to the duration_days column. For aggregations, we count the total number of observations at each duration (num_obs) and the number of subjects who experienced the outcome (i.e. made their first transaction) at that duration (events). The latter count requires a CASE statement to count the number of non-null entries in the endpoint_type field.
SELECT
duration_days,
COUNT(1) AS num_obs,
SUM(
CASE
WHEN endpoint_type IS NOT NULL THEN 1
ELSE 0
END
) AS events
FROM duration_rounded
GROUP BY 1 duration_days | num_obs | events
---------------+---------+--------
0 | 118 | 118
1 | 14536 | 9451
2 | 5860 | 379
3 | 9605 | 172
4 | 11092 | 133So far, pretty straightforward. Now things start getting a little trickier. The next CTE is cumulative_tally, which counts the number of subjects still at risk of experiencing the target outcome.
To compute this, we use a window function to get the cumulative sum of observations at all previous durations, then subtract this from the total number of subjects. The COALESCE function is needed because the cumulative sum over preceding rows is undefined in the first row.
SELECT
duration_days,
num_obs,
events,
num_subjects - COALESCE(SUM(num_obs) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND 1 PRECEDING), 0
) AS at_risk
FROM daily_tally, num_subjects duration_days | num_obs | events | at_risk
---------------+---------+--------+---------
0 | 118 | 118 | 1407580
1 | 14536 | 9451 | 1407462
2 | 5860 | 379 | 1392926
3 | 9605 | 172 | 1387066
4 | 11092 | 133 | 1377461Let’s take a look at the third row, to keep things concrete. 118 users made a transaction right at time 0 and 14,536 users made a transaction on their first day (not counting time 0) OR were censored on the first day. How could a user be censored on their first day? If they first entered the system on the last day of observation, then they’ve only been in the system for 1 day before the dataset was closed. So all we know is that it took them at least one day to make their first transaction.
So the number of users at risk of making a transaction after one full day is
which is reflected in the third entry of the at_risk column.
One other SQL wrinkle worth noting here: I broadcast the total number of subjects to each row by selecting from both the daily_tally and num_subjects CTEs. This computes the Cartesian product of the two tables, which is what we want here because num_subjects only has one field with one value.
Lastly, we need the number of censored subjects, which is even trickier. At each duration, the count of censored subjects is the number of subjects still at risk minus the number of subjects who experienced the outcome minus the number of subjects still at risk in the next duration. This is computed in the final SELECT statement:
SELECT
duration_days,
at_risk,
num_obs,
events,
at_risk - events - COALESCE(lead(at_risk, 1) OVER (ORDER BY duration_days ASC), 0) AS censored
FROM cumulative_tally
WHERE events > 0; duration_days | at_risk | num_obs | events | censored
---------------+---------+---------+--------+----------
0 | 1407580 | 118 | 118 | 0
1 | 1407462 | 14536 | 9451 | 5085
2 | 1392926 | 5860 | 379 | 5481
3 | 1387066 | 9605 | 172 | 9433
4 | 1377461 | 11092 | 133 | 10959This seems way too complicated; why not just subtract events from num_obs to get the number of censored subjects?
Here’s why. The final survival table has rows only for durations with at least one observed outcome event, implemented with the WHERE events > 0 clause. This clause comes at the end of the query syntactically but logically it comes before the aggregations in the SELECT clause. Simply subtracting events from num_obs would incorrectly ignore subjects censored at durations that are dropped from the output table.
This is easier to see in the later durations:
duration_days | at_risk | num_obs | events | censored
---------------+---------+---------+--------+----------
124 | 156580 | 11086 | 1 | 11085
125 | 145494 | 10196 | 1 | 45118
129 | 100375 | 11691 | 2 | 11689
130 | 88684 | 9011 | 1 | 9010
131 | 79673 | 6990 | 1 | 79672Between durations of 125 and 129 days, the number of at-risk subjects drops by over 45,000, but only 1 person has a transaction at 125 days. How can that be? Well, 45,118 users have censored durations of 125 days or 126-128 days (but not 129 days, that’s counted in the next row).
Survival, conversion, and cumulative hazard curves
Now that the survival table is complete, we can get to the interesting stuff. Here are the relevant aggregations again from the final SELECT statement:
SELECT
duration_days,
EXP(SUM(LN(1 - events / at_risk)) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND current ROW
)) AS survival_proba,
100 * (1 - EXP(SUM(LN(1 - events / at_risk)) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND current ROW
))) AS conversion_pct,
SUM(events / at_risk) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND current ROW
) AS cumulative_hazard
FROM cumulative_tally
WHERE events > 0; duration_days | survival_proba | conversion_pct | cumulative_hazard
---------------+----------------+----------------+-------------------
0 | 0.9999 | 0.0083 | 0.0000
1 | 0.9932 | 0.6798 | 0.0067
2 | 0.9929 | 0.7068 | 0.0070
3 | 0.9928 | 0.7191 | 0.0071
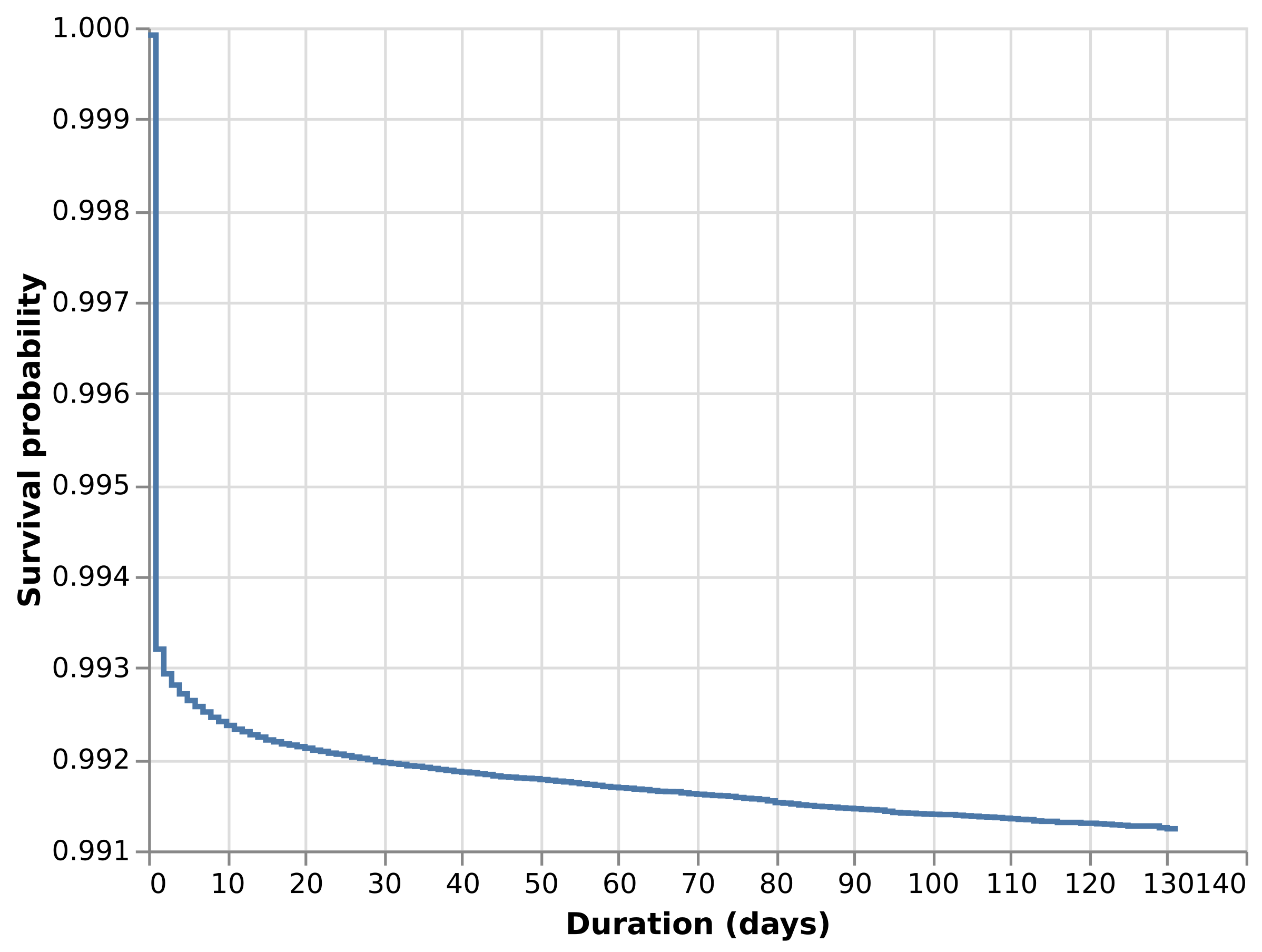
4 | 0.9927 | 0.7287 | 0.0072Kaplan-Meier survival curve
A survival curve shows the fraction of study subjects who are still “alive” at each duration. The Kaplan-Meier estimator of the survival curve is:
where
We use a window function over all preceding rows and the current row to compute the product cumulatively.
EXP(SUM(LN(1 - events / at_risk)) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND current ROW
))
Kaplan-Meier conversion curve
Because the fraction of users in this example who experience the outcome of interest is so small (but realistically so), it can be helpful to flip the survival probability upside down and call it a conversion rate (officially, the cumulative incidence function). It’s just 1 minus the Kaplan-Meier estimate, multiplied by 100 to make it a percentage.
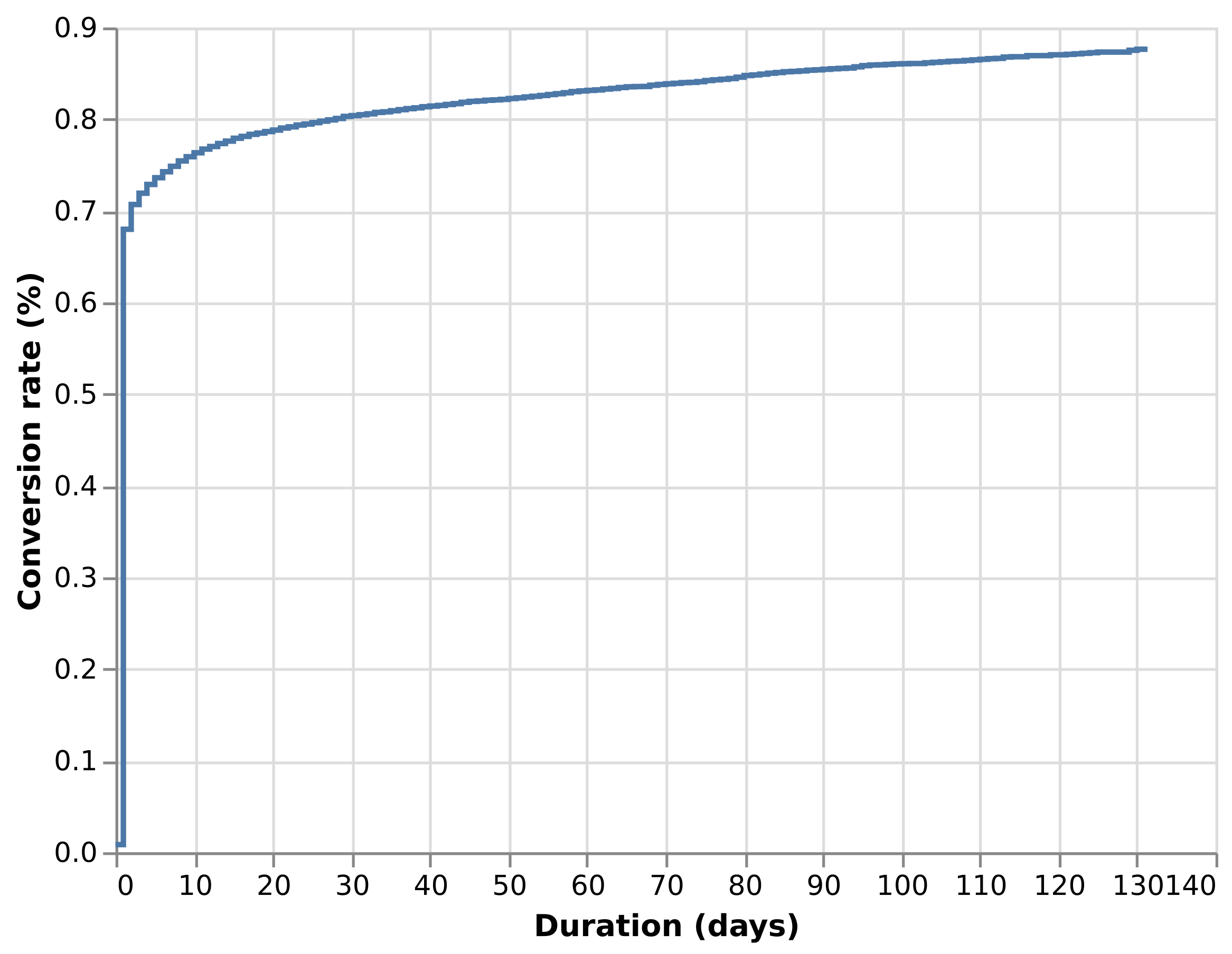
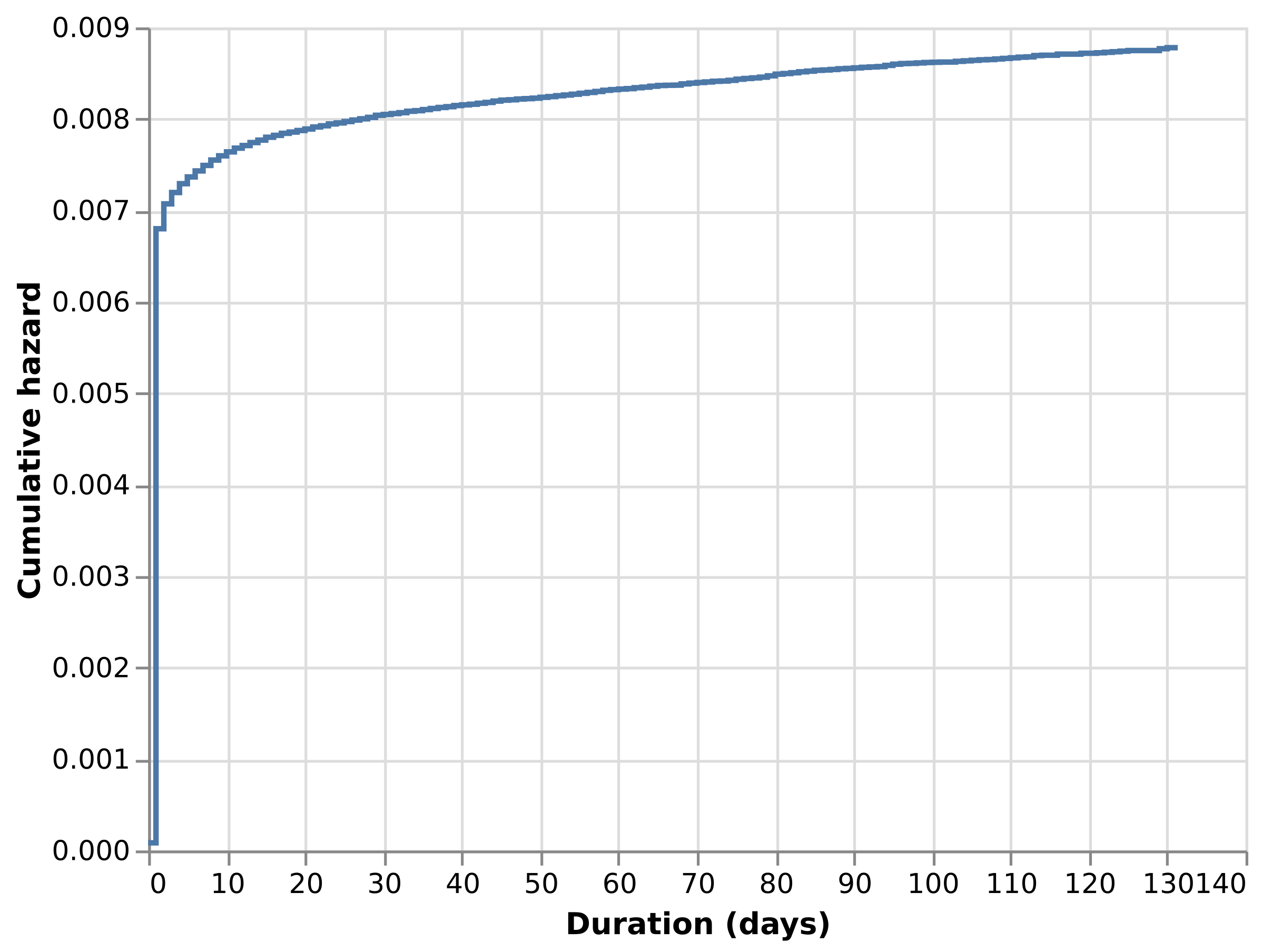
Nelson-Aalen cumulative hazard
The cumulative hazard function is another important survival analysis output. The Nelson-Aalen estimator for cumulative hazard is:
This one is easier to compute from the survival table because it only requires Postgres’s built-in SUM aggregation.
SUM(events / at_risk) OVER (
ORDER BY duration_days ASC ROWS BETWEEN UNBOUNDED PRECEDING AND current ROW
)
Final thoughts
The code above should be all you need to compute survival and cumulative hazard curves directly in your data warehouse analytics tables and analytics dashboards.
I’d love to hear about your experiences using survival analysis in the wild, especially in applications beyond clinical research. Please leave a comment or drop me a line on the contact form.
References
- Listing image by Timo C. Dinger on Unsplash.